更新日:2025年11月7日
ここから本文です。
統計を使って分析してみよう(中級編)
|
このページでは、実際の統計データを使って調べたり考えたりする方法を紹介しています。 |
 |
|
|
統計って?
私たちの身の回りには、クラスのテストの点数、身長や体重、テレビの視聴率、気温の変化など、さまざまな「データ」があります。
これらのデータを整理し、特徴をとらえ、また数量的に把握すること、またその結果として得られた数値を「統計」といいます。
統計は、国や地方自治体の政策から、コンビニなどの出店計画をはじめとした企業のマーケティング、医療や教育など、社会のさまざまな場面で使われています。
身近な統計データを調べて使ってみよう
国や地方自治体で実施されている公的統計は、結果が公表されていることが多く、さまざまな分野から地域の特徴をとらえるのに適しています。
ここでは、SSDSE(教育用標準データセット)を使ったデータ分析の手順の一例を紹介します。
使用したデータは2025年の「SSDSE-家計消費」です。このデータから、県庁所在市別の果物の年間消費額の違いについて見てみます。
データ形式は、EXCELファイルとCSVファイルがあります。今回はグラフの作成も行いたいので、EXCELファイルをダウンロードしました。
|
|
データのばらつき
基礎編では、最大値、最小値、平均値、中央値といった主な代表値を見ながらデータの全体を把握し、主にデータの大きさの比べ方について紹介しました。
ここでは、実際の分析手順の前にデータの「ばらつき」について紹介します。
たとえば、Aさん、Bさん、Cさん、Dさん4人のテストの点数の例を見てみます。
| Aさん | Bさん | Cさん | Dさん | 4人の平均点 | |
| 国語 | 70 | 70 | 70 | 70 | 70 |
| 英語 | 80 | 70 | 65 | 65 | 70 |
| 数学 | 100 | 80 | 60 | 40 | 70 |
 4人の国語、英語、数学の平均点はいずれも70点です。
4人の国語、英語、数学の平均点はいずれも70点です。
ただ、国語は全員70点と、ばらつきがないのに対し、英語は65~80点、数学は40点~100点とばらつきがあります。
また、英語に比べて、数学のばらつきが大きいことも分かります。
この「ばらつき」を数値やグラフで客観的に表現するにはどのようにすればいいでしょうか。
ばらつきを数値で測る
基準からの距離を測ってみる(偏差)
ばらつきを測るための方法として、平均からの距離(偏差)を計算してみます。
|
例:上記の数学の点数の場合 |
この偏差の合計を使えば、ばらつきの大きさを測ることができそうですが、偏差を単純に合計すると、プラスとマイナスが打ち消しあって常に0になります。
偏差を2乗して平均する(分散)
偏差の合計は常に0になるため、偏差を使ってばらつきを測るためにはマイナスを除去する必要があります。絶対値を用いる方法もありますが、統計学でよく使われるのが、偏差を2乗して平均する「分散」です。
|
例:上記の数学の点数の場合 |
分散の単位を戻す(標準偏差)
分散は点数を2乗した平均なので、単位が「点^2」となっていて、直感的に差を比較することが難しく感じることもあります(^以下は乗数を表しています)。
比較しやすくするためには、単位を元に戻す必要があるので、分散の平方根(ルート)を取ります。これを標準偏差といいます。
|
例:上記の数学の点数の場合 |
標準偏差を用いることで、元のデータと同じ単位でばらつきの大きさを評価できるようになりました。
試験でよく耳にする「偏差値」もデータのばらつき(偏差、標準偏差)を利用して自分の位置を測る指標です。
自分の得点をXとすれば、次の式で求められます。
偏差値=50+10×(X-平均)÷標準偏差
ばらつきを見える化する
箱ひげ図と四分位数
上記では「数値」でばらつきを測ってきましたが、平均値や標準偏差は極端に大きい・小さい値があると、その影響を大きく受けてしまう性質があります。
以下では、データを小さい順に並べて、その「順位」で区切ってばらつきを見る四分位数を紹介します。
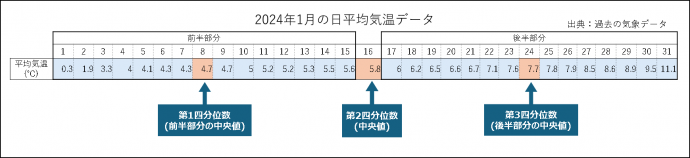
表1は、2024年の1月の京都の日平均気温データをまとめた表です。
表1_1月の平均気温(2024年,京都)

図1は、表1のデータを使って、気温の分布を表したグラフです。このようなグラフを箱ひげ図といいます。
左端の値が最小値、右端の値が最大値を表しており、中央の長方形が四分位数を表しています。
箱ひげ図は、最小値、最大値、四分位数が一目で把握できるので、データの分布を概観するときに大変便利です。
図1_1月の日平均気温(2024年,京都)

出典:過去の気象データ(気象庁)
|
図2_四分位数の解説
箱ひげ図では、長方形の長さが四分位範囲を表しています。 |
|
データの分布を見るときは、ヒストグラムも使われます。 図3は、図1と同じデータを使って作成したヒストグラムです。 |
図3_1月の日平均気温(2024年,京都)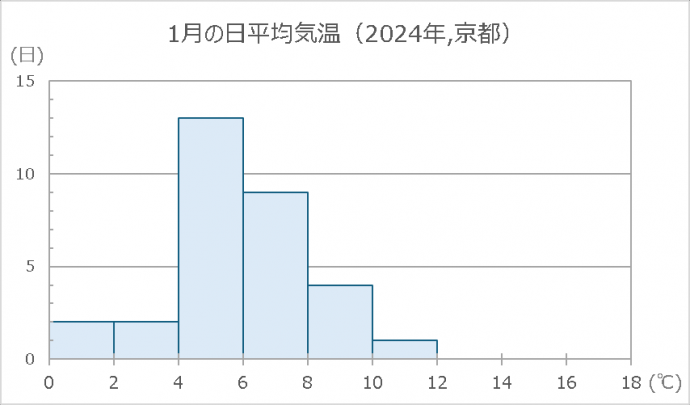 出典:過去の気象データ(気象庁) |
|
一方で、データ同士を比較するのには箱ひげ図の方が適しています。 |
|
|
図4_月別の日平均気温(2024年,京都) |
図5_1~3月の日平均気温(2024年,京都)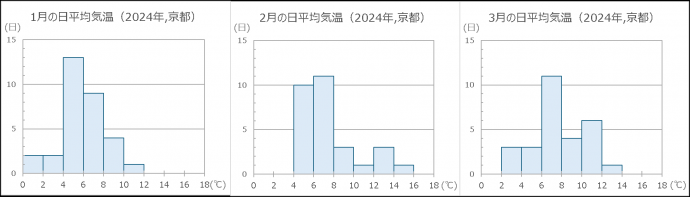 出典:過去の気象データ(気象庁) |
実際のデータで実践
四分位数を求めて箱ひげ図を作ってみよう
ここでは、上記で紹介した2025年のSSDSE-家計消費のデータから果物の年間家計消費額の違いを見てみます。
Excelを使った実際のデータの加工方法や、四分位数の求め方、箱ひげ図の作り方を詳しく解説していますので参考にしてください。
理由を考えて、他のデータも調べてみよう
りんごや桃などの果物の年間消費額は、それぞれの生産地として知られる地域で特に高くなっていることが分かりました。
都道府県別の果物の生産量と比べてみたり、地図を消費額の高い低いで塗り分けてみても新しい発見があるかもしれません。
果物以外の消費額のばらつきを調べてみるのもいいでしょう。
このページで紹介したSSDSE以外にも、国が実施している政府統計のデータを探すときは、政府統計の総合窓口e-Stat(外部リンク)が便利です。
ぜひ色んなデータを調べて、考えてみてください。
お問い合わせ
トップページ > 府政情報 > 広報・情報公開等 > 京都府の統計情報 > 統計で見る京都府のすがた > 統計を使って分析してみよう > 統計を使って分析してみよう(中級編)